Svetlana Jitomirskaya, la matemática detrás de la solución a “el problema de los diez martinis” de la mecánica cuántica

Eso, en parte, la llevó a adentrarse en un problema matemático que fue planteado en 1981.

"La mariposa de Hofstadter es un objeto extremadamente placentero de ver", dice.

Se trata de la representación gráfica, hecha en los años 70 por el científico Douglas Hofstadter, de un conjunto fractal y que ha desempeñado un rol importante en la mecánica cuántica.

Pero había algo más determinante que la atrajo al problema: "algunas ideas significativas" que ella había desarrollado en ese campo.

Además -señala- la conjetura "tiene un nombre muy atractivo".

La matemática ayudó a resolver "el problema de los diez martinis", cuyo nombre surgió después de que el matemático Mark Kac ofreciera diez martinis a quien lo solucionara.

Kac no pudo apreciar el logro de Jitomirskaya. Murió en 1984, pero su colega Barry Simon fue quien le dio el nombre a la conjetura y la popularizó.

"¿Se ha tomado alguna vez un martini?", le pregunto a la investigadora que vive en Estados Unidos.

"He tomado martinis, pero no por este problema", dice entre risas.

Esta es la historia de una de las matemáticas más destacadas de la actualidad, cuyos aportes a la física matemática y los sistemas dinámicos han sido ampliamente reconocidos.

Más recientemente, en julio, le otorgaron el primer premio Olga Alexandrovna Ladyzhenskaya, en una sesión conjunta de dos conferencias satélites del Congreso Internacional de Matemáticos.

Entre matemáticos

Jitomirskaya nació en Járkiv, Ucrania, en 1966.

Habla con admiración de su madre, Valentina Borok, una destacada matemática que trabajó en ecuaciones diferenciales parciales y que se convirtió en 1970 en la única profesora titular de matemáticas de Ucrania.

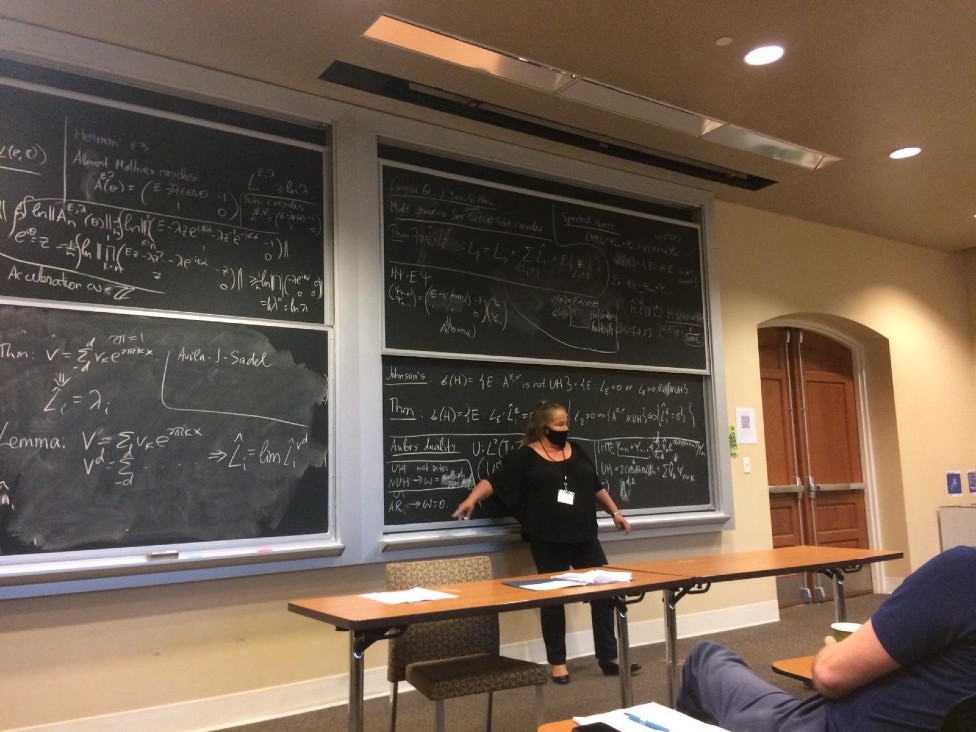
"Ella era tan brillante que yo sabía que yo no lo era tanto", cuenta.

"En cierto sentido, no pensé que podría tener éxito en matemáticas porque era muy difícil para las mujeres en ese momento".

"Estaba claro que uno, especialmente como mujer, tenía que ser muy sobresaliente, pero no porque hubiera discriminación, era porque, a pesar de toda la propaganda comunista de que las mujeres eran iguales, toda la sociedad era extremadamente tradicional y se esperaba que las mujeres se encargaran de la familia y del ámbito doméstico".

"Mi mamá siempre me decía que la familia era lo más importante".

Y, aunque fue una inspiración, sabía que su madre no quería que siguiera el camino de las matemáticas.

Su padre, también matemático, no la contradijo: "Mis padres estaban actuando como una unidad".

"Cuando era pequeña, fue como si hubiesen tratado de alguna manera de disuadirme de convertirme en matemática porque pensaban que era demasiado difícil para una niña".

"Hace poco le pregunté a mi padre por qué me desanimaron a mí y no a mi hermano y me dijo: 'Fue idea de tu mamá'. Creo que es cierto, que fue su idea de que intentaran orientarme hacia otras cosas".

Como un "milagro"

Jitomirskaya amaba la literatura y la filología, pero para ella la Unión Soviética no era el lugar ideal para seguir esa pasión ya que esos campos estaban fuertemente impregnados por la ideología comunista.

Entonces, se enamoró de las matemáticas cuando comenzó a estudiarlas profundamente, "lo que solo sucedió cuando ingresé a la Universidad Estatal de Moscú".

"Era un ambiente increíble para una estudiante que estaba lista para absorberlo todo y dispuesta a estudiar mucho".

"Y fue una especie de milagro que haya entrado porque básicamente no admitían judíos".

Se preparó muy bien para el proceso de admisión porque, dice, a los aspirantes judíos se les daba un trato muy diferente.

"Les ponían problemas muy difíciles, básicamente imposibles de resolver. Por eso, pasé mi último año de secundaria preparándome para ese examen".

Aún así, pensó que no lo pasaría.

"De alguna manera no se dieron cuenta de que era judía". Cuenta que apareció en los documentos como ucraniana.

Fue admitida y la niña de 16 años aprovechó todos los recursos educativos disponibles: "conferencias, seminarios increíbles".

"Realmente me enamoré de las matemáticas y nunca miré hacia atrás. Recuerdo que en segundo año de carrera pensé que no podía imaginarme estudiando otra cosa que no fueran matemáticas".

Años después, tras una oportunidad académica que le surgió a su esposo, quien es químico físico, Jitomirskaya se fue junto a él a Estados Unidos.

Encontró un trabajo temporal como profesora a tiempo parcial en la Universidad de California, Irvine, y siguió con sus investigaciones.

Actualmente es profesora en esa institución y recientemente fue nombrada profesora del Instituto de Tecnología de Georgia.

Física matemática

La investigadora explica que uno de los focos de su campo es probar conjeturas que hacen los físicos, "ideas que se han entendido desde hace mucho tiempo".

Pero también hace lo opuesto, "a veces refutamos, demostramos que se equivocaron, a veces haciendo nuevas predicciones relacionadas con modelos físicos".

"Es bastante emocionante porque a veces se establecen conexiones con la vida real, pero no siempre".

"Más concretamente, trabajo en el campo de los operadores cuasi periódicos".

Esto tiene que ver con la mecánica cuántica y "el problema de los 10 martinis" es parte de ese fascinante campo.

Desde los años 90, Jitomirskaya trabajó en varios aspectos de esa conjetura, consiguió muchas "piezas del rompecabezas" y publicó sus resultados.

En 2003, el matemático español Joaquim Puig "hizo un avance crucial en este problema". De hecho, en su investigación citó el trabajo de Jitomirskaya.

"Se dio cuenta de algo muy bonito. Parecía una adición pequeña a mi trabajo anterior, pero fue una observación muy brillante y estaba un poco molesta conmigo misma por no haber visto ese camino hacia el problema".

"Todos los parámetros"

Menos de un año después, un matemático brasileño "muy joven" la contactó (años después, en 2014, ese muchacho ganaría la Medalla Fields, también conocida como el Premio Nobel de matemáticas).

"Arthur Ávila me escribió que quería visitarme para trabajar en este problema. Ya había visto su nombre porque había publicado un par de artículos excelentes".

Jitomirskaya recuerda que él le dijo: "el problema no está completamente resuelto hasta que descifres todos los parámetros".

Ávila le mencionó que había visto en una de sus publicaciones que ella había insinuado que podía obtener otro resultado para los "parámetros restantes".

"Y me dijo que si realmente yo podía hacerlo, podríamos terminar el problema por completo. Le dije que se podía hacer, pero que sería muy difícil, técnico, y que tomaría mucho tiempo".

Pero, Ávila fue persuasivo.

Cuando empezaron a trabajar en "esta demostración técnica tan difícil", se dieron cuenta de que tenían que "inventar otras vías".

Y en ese proceso, desarrollaron herramientas, técnicas y enfoques nuevos que son admirados por los conocedores.

Demostraron la conjetura y publicaron el resultado en la prestigiosa revista Annals of Mathematics en 2009.

¿De qué se trata el problema?

Daniel Peralta es investigador especializado en sistemas dinámicos del Instituto de Ciencias Matemáticas (ICMAT) en el Consejo Superior de Investigaciones Científicas (CSIC) de España.

Conoce el trabajo de Jitomirskaya, con quien ha coincidido en varios congresos. "Siempre es muy agradable conversar con ella y escuchar sus presentaciones", le dice a BBC Mundo.

De hecho, recuerda una conferencia en China cuando la matemática mostró la mariposa de Hofstadter, que representa el espectro de los operadores que ella estudia.

Esos operadores -explica Peralta- surgen en ciertos modelos que buscan describir fenómenos físicos de tipo cuántico.

"Los operadores de Schrödinger aparecen en muchos contextos de mecánica cuántica y Jitomirskaya ha estudiado principalmente los que aparecen en el contexto del movimiento de electrones sujetos a campos magnéticos perpendiculares a la dinámica del electrón".

Se conocen como operadores de Mathieu cuasiperiódicos.

"En general un operador de la mecánica cuántica es un objeto matemático, una regla matemática, que toma una función de diferentes valores y devuelve otra función distinta".

La clave es entender, desde el punto de vista físico, el espectro, es decir, ver para qué funciones, cuando el operador se aplica a ellas, devuelve la misma función.

Esa, explica el investigador, es una de las grandes diferencias (entre muchas otras) de la física clásica y la física cuántica.

Por ejemplo, en principio, en la física clásica la velocidad de un electrón, de una partícula, puede tomar cualquier valor.

"Sin embargo, en mecánica cuántica, hay muchos objetos que están cuantizados, no pueden tomar cualquier valor, solo pueden tomar una serie de valores discretos. Este fenómeno, junto con el principio de incertidumbre de Heisenberg (esto es, el hecho de que ciertas magnitudes no pueden ser medidas con precisión) marcan la diferencia principal con respecto a la física clásica".

La demostración

En los años 60, los físicos vieron que los valores que puede tomar este tipo de operadores depende de la frecuencia, es decir, que el espectro cambia cuando los parámetros varían.

"Observaron que cuando la frecuencia era (un número) irracional, el espectro tenía una estructura muy extraña, fractal, y eso se conoce como un conjunto de Cantor".

"Esto se plantea de forma matemática en el enunciado de los diez martinis".

El problema consiste en probar -lo que los físicos ya habían observado- que cuando la frecuencia, es decir, la intensidad del campo magnético para este tipo de operadores es un número irracional, el espectro es un conjunto de Cantor.

Desde los años 80, 90, muchos investigadores trabajaron en ese problema.

Puig hizo un gran avance, pero "la cumbre de todo ese trabajo, de años y de tantas personas, es la demostración a la que llegaron Ávila y Jitomirskaya".

"Ellos prueban la conjetura original: para todas las frecuencias irracionales, el espectro de los operadores de Mathieu cuasiperiódicos es un conjunto de Cantor.

Así queda resuelto finalmente 'El problema de los diez martinis'".

Esta nota forma parte del especial de la BBC con 100 mujeres inspiradoras e influyentes del mundo en 2022.

Ahora puedes recibir notificaciones de BBC Mundo. Descarga la nueva versión de nuestra app y actívalas para no perderte nuestro mejor contenido.

• ¿Ya conoces nuestro canal de YouTube? ¡Suscríbete!